Explaining the Type SAM Multiplier
Multipliers
Technically, a Multiplier is unit-less because it is calculated as follows:
- Output Multiplier = Total Output / Direct Output
- GDP Multiplier = Total GDP / Direct GDP
- Employment Multiplier = Total Employment / Direct Employment
This is why the IMPLAN Multiplier reports differentiate between Effects, which are on a per-million-dollar basis (e.g., a Direct Employment effect of 7.5 indicates that 7.5 Direct jobs are needed for $1 million worth of production in that Industry), and Multipliers, which are unit-less (e.g., an Employment Multiplier of 2.5 indicates that 1.5 additional Indirect and Induced jobs in a variety of Industries are needed for every Direct job in that Industry).
The Output of any given Industry (Xi) goes to meet intermediate demands for the Industry (XiAi), where Ai represents the production function for Industry i, plus Final Demand for the Industry (Yi). That is, the Output of Industry i (Xi) depends on all other Industries’ Output (X) times their requirements for Industry i’s Output as one of their inputs (as determined by their production functions, (A)), plus the Final Demand for Industry i’s Output (Yi). Thus, if X = the matrix of all Industries’ Output and Y = the matrix of Final Demand for all Industries and A = the matrix of production functions for all industries, then X = AX + Y. Solving for Y we get Y = X (I-A)-1. (I-A)-1 is known as the Leontief Inverse. For any one particular Industry this equation becomes Yi = Xi (I-A)-1. This equation tells us the Output of each and every Industry that is required to meet Final Demand of Industry i. If we wanted to know how much each Industry’s Output would change in response to a change in the Final Demand of Industry i, we would modify the equation to ∆Yi = ∆Xi (I-A)-1. In other words, to meet a change in the Final Demand for Industry i (∆Yi) we need to increase that Industry’s Output (∆Xi) plus the Output of that Industry’s input suppliers (∆Xi*A).
Type I Multiplier
A Type I Multiplier is calculated by dividing the sum of the Direct Effects (the change in Final Demand that the analyst inputs into IMPLAN) plus the Indirect Effects (the additional economic activity from Industries buying from other local Industries) by the Direct Effects.
Type SAM Multiplier
A Type SAM Multiplier (where SAM stands for Social Accounting Matrix) is calculated by dividing the sum of the Direct Effects, Indirect Effects, and Induced Effects by the Direct Effects. The Induced Effects represent the spending of Labor Income by the employees working in the Indirectly-impacted Industries, under the assumption that the more income households earn, the more money those households spend. Note that IMPLAN does not assume that 100% of this Labor Income is spent, nor that it is spent locally. IMPLAN removes payroll taxes, personal income taxes, savings, in-commuter income, and non-local purchases before spending the rest locally. These leakages and expenditures are based on information in the SAM.
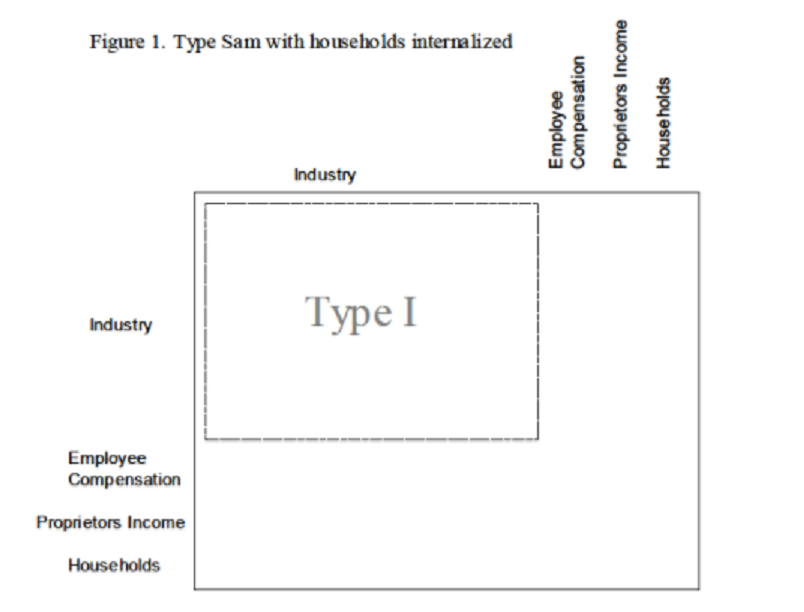
Type SAM Multipliers with Households Internalized
Theoretically, you could internalize any of the Institutions (households, government, and capital), but the standard practice (and the default in IMPLAN) is to internalize households only; that is, to capture the household spending of Labor Income but not the spending of tax revenues or returns to capital (Figure 1).
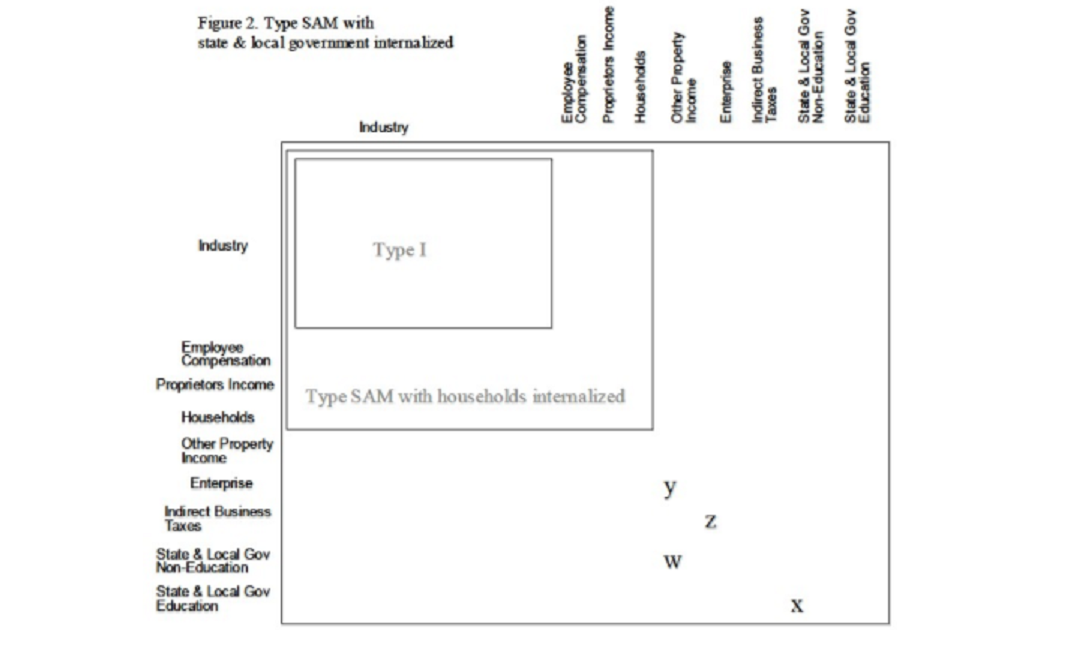
Type SAM Multipliers with State and Local Government Internalized
Internalizing State & Local Government Education and Non-education assumes that these Institutions will re-spend each dollar of local tax, fee, licenses, etc. collected locally for local programs. In a state model this makes sense – state budgets are required to be balanced, so the more they collect the more they spend and vice-versa (the occasional state tax rebate complicates this but it tends to be the exception rather than the norm). At the local level, however, this becomes more problematic; while the locally-collected tax dollar goes to the state general pot, the local region tends to receive equal money back (the occasional newspaper article pops up regarding a local legislator complaining that his district is not receiving its fair share of state revenue. Likewise, a declining region will receive more than its fair share of unemployment compensation and economic development funds).
Figure 2 helps illustrate the mechanics of internalizing State & Local Government. First note that we have introduced Other Property Income (OPI), which is mostly corporate profits, and Enterprises, which is mostly retained corporate profits. These have been included because for some states corporate taxes are an important source of government income. There is a direct transfer of interest (either net positive or negative) marked as “w” in Figure 2 from OPI to Government. There is also a transfer from OPI to Enterprises (the source of retained earnings) – marked “y” in Figure 1 and the transfer from Enterprises to State and Local Government Non-Education (corporate income taxes) – marked “z” in Figure 2.
Taxes on Production & Imports (sales taxes, property taxes, licenses, etc.) represent one of the most important sources of income for State and Local Government. Note that payroll taxes and personal income taxes are already part of the default formulation with households internalized. If including a State and Local Government Institution, it is almost necessary to include both Non-Education and Education together in the formulation because a large portion of State and Local Non-Education spending is an appropriation to Education. In IMPLAN, only the Non-Education Sector collects money, so Education is only funded by an appropriation. If internalized by itself, this would not add any impact to the Induced Effects. Thus, without Education, a large portion of the Non-Education spending would be leaked.
However, the case for State and Local Government Investment is not as straightforward. While much of Government Investment is operational capital goods (trucks, computers, etc.), very large projects (highways, buildings, stadiums, etc.) are funded through bonding and are not necessarily related to the current state of the economy. IMPLAN is not aware of any studies in which Government Investment is internalized as part of a Type SAM Multiplier.
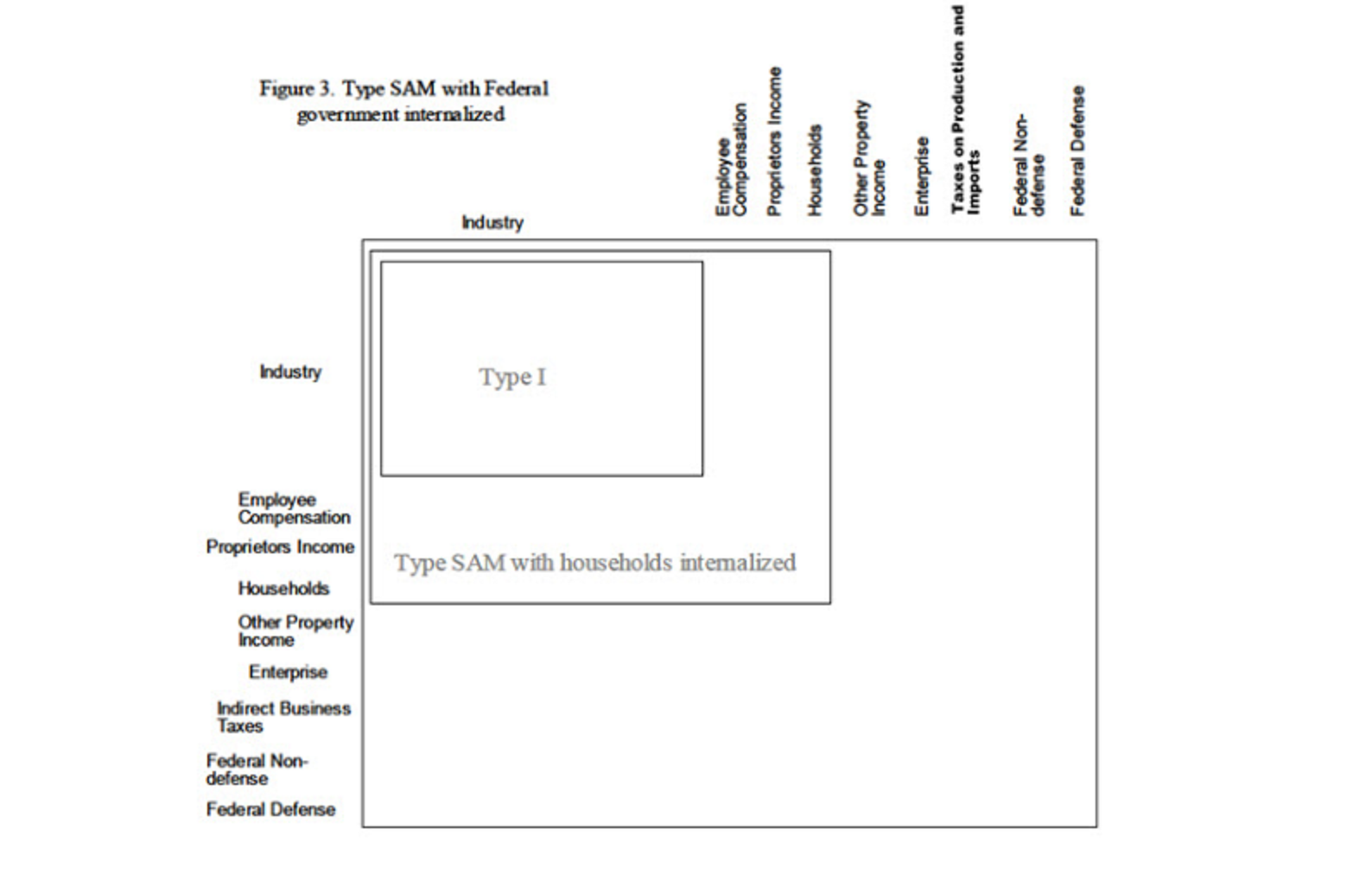
Type SAM Multipliers with Federal Government Internalized
Internalizing Federal Government is similar to internalizing State and Local Government in that it assumes that each dollar of locally-collected Federal taxes will be re-spent locally. The only situation where internalizing Federal Government can be safely justified is in a national Model. Many Federal Non-Military services are based on population and some argument could be made to include it, but the ability of more powerful representatives to direct appropriations render this assumption questionable at the local level. When it comes to Federal Military, a locally growing economy will cause little Indirect or Induced growth on the local military base, rendering this assumption questionable at the local level as well. The formulation of the type SAM Multiplier with Federal Government internalized (Figure 3) mirrors that with State and Local Government internalized. Federal Non-Military funding comes from taxes paid by Households, Taxes on Production & Imports (TOPI), corporate income taxes, and net interest payments from OPI. One increasingly significant source of Federal funding is Capital (i.e., borrowing). However, Federal borrowing is not linearly related to the economy, so it is not included as part of the type SAM Multiplier. Similar to State and Local Education (above), Federal Military is only funded by appropriation from Federal Non-Military, so by itself would not add to the Induced Effect.
Internalizing Federal Government Investment is even more tenuous than State and Local Government Investment. Federal Investment is likely to be more directly related to the party and seniority of the representative or the occurrence of a disaster than local economic conditions. Local economic factors figure very little in Federal spending decisions, except to the extent that population (i.e., voters) grow and decline. Since a Federal response to a new local factory is unlikely, we cannot recommend internalizing any Federal Institution.
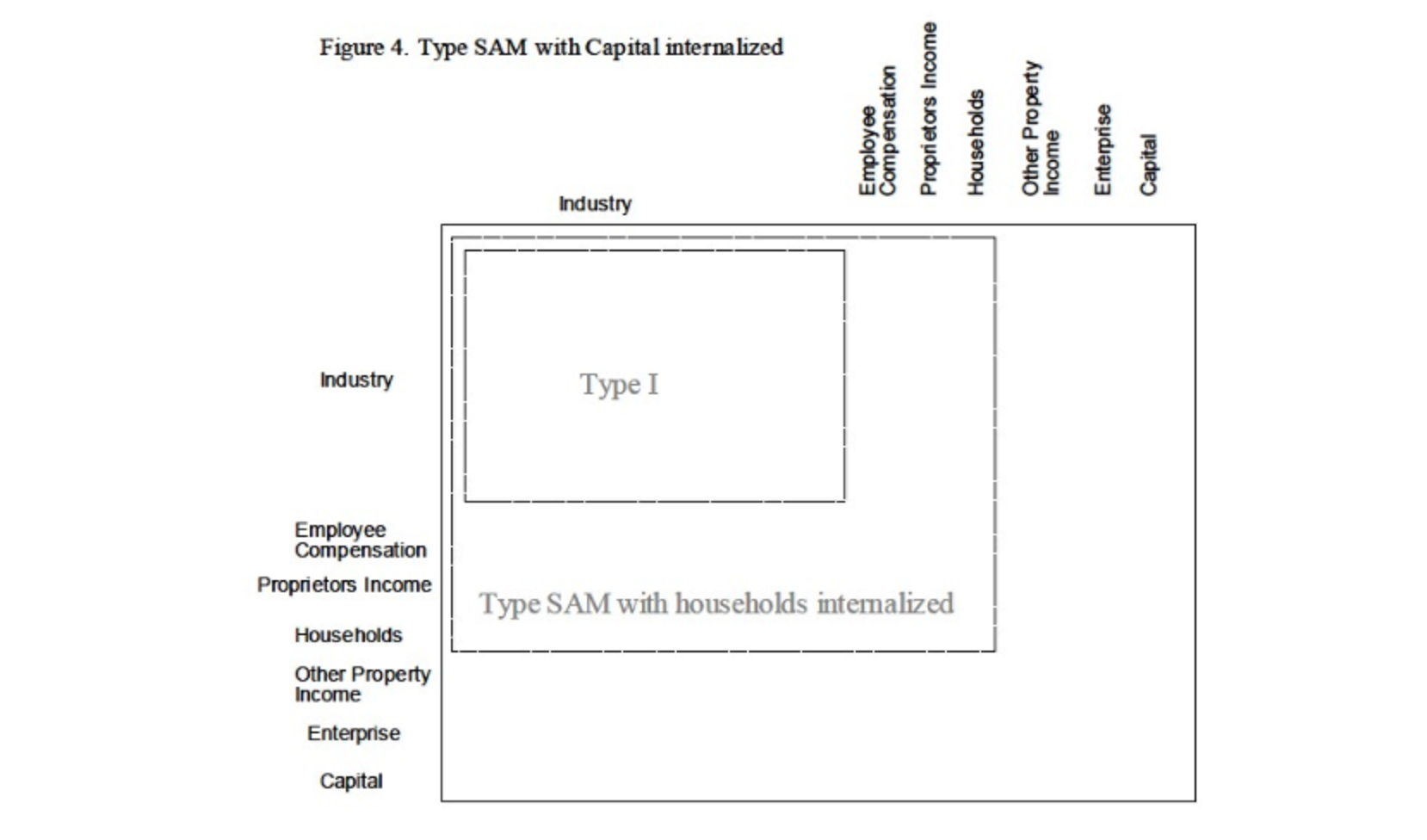
Type SAM Multipliers with Capital Internalized
Capital formation (purchase of new structures and capital equipment) is not part of any Industry production function. These purchases are a separate Institution forming one of the components of Final Demand. Final Demand is the final consumption of a good for the region – goods and services that are part of capital formation have met their ultimate use. Buildings and equipment are not re-manufactured creating new Value Added (however, they can be resold as used goods).
Industry decisions to invest are based on local conditions and perhaps the business cycle. If conditions are correct, they will invest (a non-linear action) with the promise of using a future stream of increased Value Added to pay off the investment. What this means is that when you cause an impact, increasing the Induced demand for restaurant Output (for example), we get the Employment, income and operational spending to run the restaurant but the Multipliers do not incorporate any economic activity associated with the construction of the restaurant.
Figure 4 shows the formulation of the Type SAM Multiplier with Capital Internalized. Sources of income for capital come from Industries (in the form of sales of scrap and used goods), from Households (in the form of sales of scrap and used goods and savings) and from Enterprises (in the form of savings from Other Property Income retained earnings).
As a region grows, you would expect investment to grow accordingly – but invetment is not based on local saving, but is a function of business cycle and how mature (how much of its infrastructure needs are in place) the region is. Also, this really could only possibly work in the growth direction. As a region declines, its savings decline, which would force the Multipliers to respond to negative investment.
The only rationale for negative investment is the curb on growth excess capacity has on regional investment when the region starts to grow again.
Type SAM Multipliers with Enterprises (Corporations) Internalized
There is no real spending pattern for retained earnings other than distribution to owners, government, and savings. As such, it may be useful to internalize Capital together with those Institutions but not on its own. At the local level, owners are quite likely to live outside of the region, which is why it is not standard practice to internalize this Institution.
Type SAM Multipliers with Inventory Internalized
Changes in inventory levels allow for calculating Gross Regional Product and for balancing production with sales but have no real economic impact interpretation if internalized.